Overview
Asphalt mixture is the most used material in pavement engineering. Due to its complexity, i.e., heterogeneity, granularity, temperature-dependence, etc., the mechanistic design of asphalt mixture/pavement remains a major scientific challenge. My research focuses on developing analytical and numerical models for the mechanical behaivors (e.g., compaction, cracking, rutting) of asphalt mixtures by continuum mechanics, probabilistic methods, and computational mechanics, with the aim of providing tools for the design of asphalt mixture/pavement, and granular material in general.
My current research includes the following topics:
Physical Mechanisms of Compaction
Compaction represents the most critical step in the construction process of asphalt pavements, which has a significant consequence on the durability of asphalt pavements. Due to the complexity of the asphalt mixture, we still have a limited understanding on its compaction process. The objective is to develop physics-based models for the compaction process of asphalt mixtures.
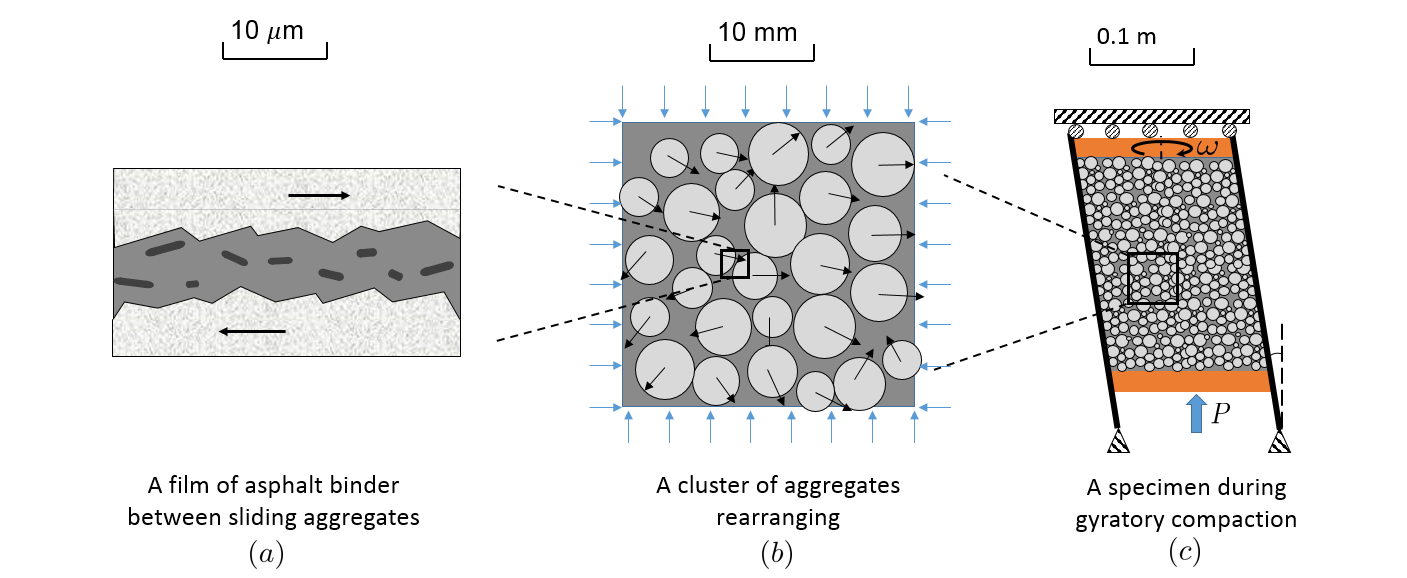
Asphalt mixture is a multiscale material, and its compaction process involves different material length scales, as shown in Fig.1. The compaction process we observed at the macroscale (Fig.1(c)) is a governed by the physical mechanisms in finer length scales. At the mesoscale (Fig.1(b)), movements of aggregates lead to the macroscopic phenomena compaction process. At the microscale (Fig.1(a)), the lubricating behavior of asphalt binder governs the relative motion between aggregates.
Mesoscale: Aggregate Rearrangement
The macroscopic compaction process is explained by the aggregate rearrangements at the mesoscale. Under static compression, aggregates would jam to a loose packing state. Under compression with excitation like shear or vibration, aggregate system would evovle to denser jammed states, causing the densification of the material. Interpreted from an energy point of view, aggregate rearrangement is a state transition process between adjacent energy wells in the energy landscape, as shown in Fig.2. This interpretation explains the effect of shear and vibration on enhancing compaction, shape of the gyratory compaction curve, and the change of shear resistance during compaction.

Related publications: RMPD 2021
Related presentations: EATA 2021, ASCE Pavement 2021
Microscale: Tribology of Asphalt Binder
Tribological property of liquid asphalt binder affects the relative motion between aggrgates, and thus affects the compaction of asphalt mixture. A tribological test was developed to measure the lubricating effect (friction coefficient) of a thin asphalt binder film between rough solid surfaces, which simulates the interaction between binder and aggregates during compaction process. Tribologial and viscosity tests were performed on graphite nanoplatelets (GNP) modified asphalt binders. The results showed that, compared to viscosity, the tribological property (friction coefficient) of asphalt binder is more related to compactability of mixtures, which implies that lubricating effect of asphalt binder may represents a more comprehensive mechanism explaining the effect of asphalt binder on compaction than binder viscosity.

Related publications: Materials 2020
Related presentations: TRB 2020
Modeling of Gyratory Compaction
Although there have been empricial models (e.g., locking point, energy indices) and high fidelity computational models (e.g., based on FEM and DEM) for gyratory compaction of asphalt mixtures, some foundmental questions about gyratory compaction still remain. For example, 1) why the density is higher in the middle while lower at the two ends, as shown in the density profile Fig.4(a)? and 2) why larger specimens are easier to compaction than shorter ones, as shown in the gyratory compaction curves Fig.4(b)? The objective is to explain these phenomena by developing physics-based model for gyratory compaction.

One-Dimensional Nonlocal Model
We simplied gyratory compaction as a one-dimensional (1D) problem (Fig.5(a)). Compaction process is interpreted as a state transition process of a cluster of aggregates (Fig.5(b)). Therefore, the transition rate theory is apply to estimate the rate of densification. The model involves a characteristic material length scale, i.e., the size of the cluster, which characterize the nonlocal interaction of aggregates in the cluster, and gives rise to strong effects of specimen height on the overall compaction curve as well as on the density profile. The proposed model was validated by a set of gyratory compaction tests of different specimen heights. The model is capable to simulate the "inversed bathtub" shape of the density profile (Fig.5(c)), and the effect of specimen height on compaction process (Fig.5(d)).

Related publications: ASCE JEM 2022
Related presentations: COTA CICPT 2021
Stochastic Modeling
As a heterogeneous material, the behaviors of asphalt mixture exhibits considerable randomness. Effect of randomness on compaction process is studies by the 1D nonlocal model for gyratory compaction. The initial density profile is assumed as a Gaussian random field. A simulation of compaction process is shown in Fig.6(a). Monte Carlo simulations were performed to study the evolution of the randomness during the gyratory compaction process. The simulation shows that the varability of compaction curve decreases with the increase in number of gyration and the decrease in specimen size, as shown in Fig.6(b), which are phenomena consistent with experimental results.

Related publications: in preparation
Related presentations:
Data Mining to Understand Field Density
High field density is desired for increasing the durability and extending the service life of asphalt pavements. In this research, we leverage the big data from construction qaulity control, and apply data mining techniques to reveal the correlations of field density with mix design indices and material composition. The results indicate strong effects of Ndesign, aggregate size (NMAS), and fine aggregate angularity on field density. For example, the effect of Ndesign on field density is show in Fig.7. It was found that the average field density is achieved at about 30 gyrations in gyratory compaction.

Probabilistic Model for Field Density Distribution
Field Density asphalt pavements exhibits considerable randomness. To understand the uncertainty is of crucial importance for building more durable pavements. We noticed that the probability distribution of field density does not follow normal distribution, since it is always left-skewed and leptokurtic. We developed a probabilistic model for field density distribution based on the mechansitic modeling of gyratory compaction and the consideration of the randomness in compaction effort. It is shown that the proposed probabilistic model explains the left-skewed and leptokurtic features of field density distribution, and it gives a more accurate prediction of the field density distribution than the normal distribution model does, especially for low density values, as shown in Fig.8.

Related publications: in preparation
Related presentations: TRB 2022